Liu & Zenner method

The basic formula is very complicated:

Four different fatigue limits f-1, f0, t-1 and t0 are needed for setup of all necessary material constants:

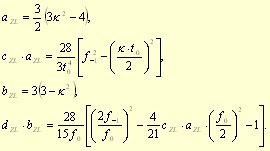
The dependency of the criterion on four material parameters was criticized by Papadopoulos in [PDG97] and led him to exclusion of the criteria from his comparison. Zenner et al. opposed his objections in [ZSL00] with a reference to common methods used for the derivation of fatigue limits in repeated loading from their fully reversed counterparts.

NOTIFICATION: Determination of the value of fatigue limit in repeated axial loading can be done in different ways – [ZSL00] e.g. uses another known value (mean stress sensitivity). There are many other different approaches how to get the fatigue limit in repeated axial loading, while no general formula can be used – see [Ppg05] for information.

Knowledge of fatigue limit in repeated torsion is even more rare. I do not know any more comprehensive analysis of its determination. Thus, if the value is not set in PragTic (input zero as the TORS0 parameter), the following formula given in [ZSL00] is used automatically:

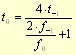
The authors [ZSL00] claim the criterion to be valid within the bounds:

The only really significant source of validity of this criterion is the FatLim Database, data provided by Zenner et al. in [ZSL00] are unclear.

Nomenclature:

Mark	Unit	PragTic variable	Meaning
	[MPa]		shear stress amplitude on an examined plane
	[MPa]		mean shear stress on an examined plane
	[MPa]	TENS-1, BEND-1	fatigue limit in fully reversed axial loading
	[MPa]	TENS0, BEND0	fatigue limit in fully repeated axial loading
	[-]		ratio of fatigue limits ()
	[MPa]		amplitude of normal stress on the plane examined
	[MPa]		mean (average value of maximum and minimum values) normal stress on the plane examined
	[MPa]	TORS-1	fatigue limit in fully reversed torsion
	[MPa]	TORS0	fatigue limit in repeated torsion

Methods & Options & Variables of Calculation – Edit

Decomposition

- Whole load path

Elasto-plasticity

- No – currently no option implemented

Solution option

- Searched planes <0~BS algorithm, 1~globe analogy, 2~random>

- Number of scanned planes

- Only every x-th data-point taken from load history

- Evaluate envelope curve only <1~yes, 0~no>

Solution variable

- Minimum damage – this option is not active for this high-cycle fatigue method

Material parameters

E	[MPa]	tensile modulus
NU	[-]	Poisson’s ratio
TENS0	[MPa]	fatigue limit in repeated tension (or plane bending)
TENS-1	[MPa]	fatigue limit in fully reversed push-pull (or plane bending)
TORS-1	[MPa]	fatigue limit in fully reversed torsion
TORS	[MPa]	fatigue limit in fully repeated torsion (see the text above, if not available)

Result detail variables

Damage fatigue index is computed, not the damage as a reciprocal value to number of cycles or repetitions

FDD1 MAXDP maximum of damage parameter

FDD2 NCX x-coordinate of the normal line vector of the plane with MAXDP

FDD3 NCY y-coordinate of the normal line vector of the plane with MAXDP

FDD4 NCZ z-coordinate of the normal line vector of the plane with MAXDP

FDD5 ALFA angle between the normal lines to the critical plane and to the free surface

This help file has been generated by the freeware version of HelpNDoc